The Newsvendor Model
How a leading sportswear manufacturer trades off the cost of having too much against the cost of having too little

In this consulting project, I advised the CEO of one of the worldwide leading sportswear manufacturers by applying the Newsvendor Model on how to calculate the optimal order quantity for a single-period product, sunglasses, to mitigate product underages or overages.
The CEO the worldwide leading sportswear manufacturer is investing to expand its product portfolio. The CEO wants her customers to purchase custom-made sunglasses with the sportswear manufacturer logo. These will be sold to customers at the affordable price of $30.
Wishing to capitalise on the idea, several founded a start-up, aiming to supply sunglasses for sportswear brands. Their goal is to demonstrate the concept at the sportswear manufacturer before rolling out to other sportswear manufacturers that start similar expansion programmes.
The sportswear manufacturer decided to support the Founders, who have already lined up investors, booked production capacity with a reputable manufacturer, come up with interesting designs, and put together an impressive business plan. The sportswear manufacturer expect that demand for sunglasses will have a mean of 3,000 units in any given year, with a standard deviation of 1,200 units. They have shared their forecast with the start-up.
The start-up’s production cost is $6 per unit. The Founders are split about which offer to make the sportswear manufacturer. Those favouring simplicity are suggesting Option 1, those favouring a more elaborate approach are suggesting Option 2:
Option 1. The start-up offers a simple wholesale price of $18 for each unit. In this case, the sportswear manufacturer will dispose of any unsold units at the end of the season as a new set of glasses will be required for the next year.
Option 2. The start-up offers to set its wholesale price at $18 (same as option 1) and agrees to credit the sportswear manufacturer $10 for each unsold unit returned to the start-up at the end of the selling season. This is known as a ‘buy-back’ contract. Since styles change each year, there is essentially no value in the returned merchandise.
Those Founders opposing Option 2 are saying that it makes no sense to pay more to buy back unsold units than it cost to manufacture them.
The CEO and the start-up’s Founders brought me onto the project to advice them on the following issues.
1. Optimal order quantity Option 1
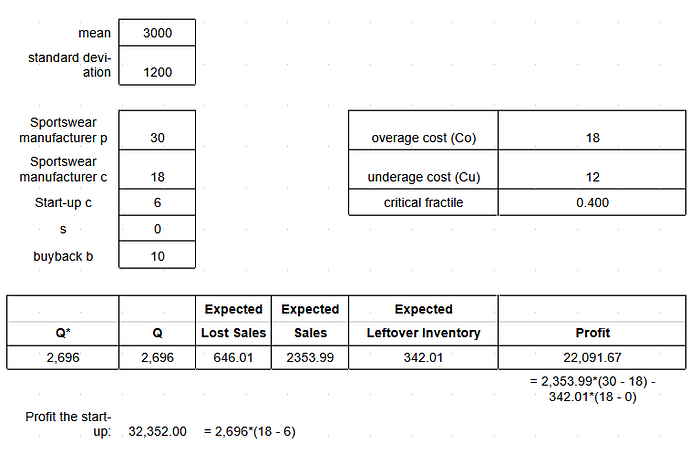
They asked me how many units the sportswear manufacturer should buy if it chooses Option 1 purely from a profit perspective. I advised them that the sportswear manufacturer should buy 2,696 units (optimal order quantity) if it chooses Option 1.
We have p = $30, c = $18. There is no salvage value(s) for unsold units.
Then,
Cu = p — c = $30 — $18 = $12. Co = c — s = $18 — $0 = $18.
The underage costs are less than the overage costs so the sportswear manufacturer should order less than the mean demand.
The critical fractile is given by
𝐹 = Cu/(Co + Cu) = $12/($18 + $12) = 0.4
The optimal quantity is Q* = 2,696 for an expected profit of $22,091.67 according to the Newsvendor Model
= 2,353.99*($30 — $18) — 342.01*($18 — $0).
The start-up will make a profit of
2,696*($18 — $6) = $32,352.
2. Optimal order quantity Option 2
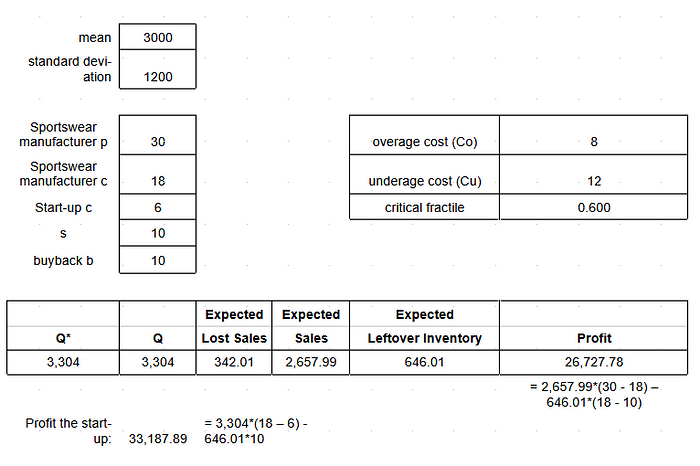
The CEO and the start-up’s Founders asked me for advice how many units the sportswear manufacturer should buy purely from a profit perspective if it chooses Option 2. I gave the recommendation that the sportswear manufacturer should buy 3,304 units (optimal order quantity) if it chooses Option 2.
We have p = $30, c = $18. The salvage value of the sportswear manufacturer for unsold units is $10 and the buyback value of the start-up is $10. Option 2 means that the sportswear manufacturer gets $10 for each unsold units from the start-up because the start-up “finances” these.
Then,
Cu= p — c = $30 — $18 = $12.
Co = c — s = $18 — $10 = $8.
The underage costs are more than the overage costs, so the sportswear manufacturer should order more than the mean demand.
The critical fractile is given by
𝐹 = Cu /(Co + Cu) = $12/($8 + $12) = 0.6
The optimal quantity is Q* = 3,304 for an expected profit of $26,727.78
= 2,657.99*($30 — $18) — 646.01*($18 — $10).
The start-up will make a profit of
3,304*($18 — $6) — 646.01*$10 = $33,187.89.
3. Expected profit
They asked me what the expected profit of the sportswear manufacturer and the start-up would be for each option. The CEO asked me which option she should prefer purely from a profit perspective. The Founders asked me which option they should prefer. For the profit calculation, please see chapter 1 and 2 above.
The expected profit for Option 1 would be for
- the sportswear manufacturer: $22,091.67
- the start-up: $32,352.00
The expected profit for Option 2 would be for
- the sportswear manufacturer: $26,727.78
- the start-up: $33,187.89
The CEO should prefer Option 2 because the sportswear manufacturer has a bigger profit in Option 2 than in Option 1. The Founders should prefer Option 2 because the start-up has a bigger profit in Option 2 than in Option 1. Both parties are better off in Option 2.
4. Optimal order quantity for Integrated Firm
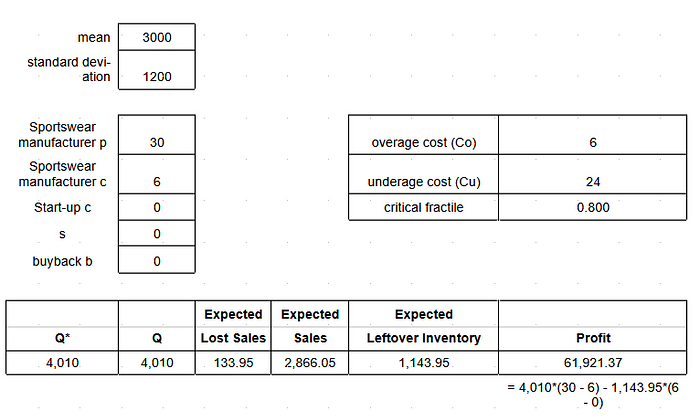
The CEO of the sportswear manufacturer assesses to acquire the start-up business to form an Integrated Firm. The CEO asked me how many units this Integrated Firm should order from the manufacturing plant purely from a profit perspective. She asked for recommendation on how much expected profit that would result in for the Integrated Firm. She wanted to know how the Integrated Firm profit compares to the total profit made by the sportswear manufacturer and the start-up with Option 1. In addition, she asked for advice how the Integrated Firm profit compares to the total profit made by the sportswear manufacturer and the start-up with Option 2
We have p = $30, c = $6. There is no salvage value and buyback value.
Then,
Cu = p — c = $30 — $6 = $24. Co = c — s = $6 — $0 = $6.
The underage costs are more than the overage costs, so the sportswear manufacturer should order more than the mean demand.
The critical fractile is given by
𝐹 = Cu/(Co + Cu) = $24/($6 + $24) = 0.8
The optimal quantity is Q* = 4,010 for an expected profit of $61,921.37
= 4,010*($30 — $6) — 1,143.95*($6 — $0).
a. Comparison Integrated Firm profit vs. total profit made by the sportswear manufacturer and the start-up with Option 1
The expected total profit for Option 1 would be
Total profit $54,443.67 = sportswear manufacturer $22,091.67 + start-up $32,352.00 < NewCo Profit $6,1921.37
The Integrated Firm profit is higher than the total profit made by the sportswear manufacturer and the start-up with Option 1.
b. Comparison Integrated Firm profit vs. total profit made by the sportswear manufacturer and the start-up with Option 2
The expected total profit for Option 2 would be
Total profit $59,915.67 = sportswear manufacturer $26,727.78 + start-up $33,187.89 < NewCo Profit $61,921.37
The Integrated Firm profit is also higher than the total profit made by the sportswear manufacturer and the start-up with Option 2.
5. Benefits and downsides of Integrated Firm
The CEO asked me to ignore profit for a moment and to list one benefit and one downside for the sportswear manufacturer of acquiring the start-up.
Benefit. One benefit for the CEO is that by acquiring the start-up the sportswear manufacturer reduces the uncertainty involved and therefore the profit increases. Consequently, less expected lost sales are ordered. The result of the acquisition is less standard deviation and therefore less uncertainty e.g., the forecast is narrower to the mean demand. In contrast, the profit decreases with higher uncertainty.
Downside. One downside of acquiring the start-up for the CEO is that like in the example of Nintendo, the sportswear manufacturer might be “under-ordering” and ordering less than the expected demand, respectively. Because in the Newsvendor Model an acquisition reduces uncertainty, the sportswear manufacturer orders more than the mean demand. But the Model does not take acquisition synergies into account. Therefore, the sportswear manufacturer would not just underage itself by producing more than the demand but also underage the synergies in cost savings and revenue enhancements. Consequently, one downside of the acquisition in this Model is to underestimate what underage cost would be.
6. Optimal order quantity in partnership
Based on my strategic recommendations the CEO of the sportswear manufacturer acquired the start-up. The mechanical engineering department of a sportswear manufacturer competitor approaches the CEO of the sportswear manufacturer with the following offer. “There is a good chance that the quantity you order from your manufacturing plant will not be enough for the customers who want to buy your product. If you partner with us and give us your designs, we can 3D print the glasses for you on the spot when customers come to your stores. We will only charge you $20 per sunglass.”
The CEO asked me to assess she would order more sunglasses or fewer sunglasses from their manufacturing plant, relative to beforehand if she were to partner with the Mechanical Engineering department. She asked me to assess if the sportswear manufacturer would make less or more profit.
The offer 3D printing solves the problem of complexity in the supply chain of the Integrated Firm and therefore the problem of uncertainty. Due to the 3D printing there is no uncertainty involved in the order planning because the mechanical engineering department 3D prints the glasses on-demand at the moment when sales are made.
In chapter 6 here, the quantity is Q = 3,000 for an expected profit of 3,000*($30 — $20) = $30,000.
In chapter 4 of the Integrated Firm, the optimal quantity is Q* = 4,010 for an expected profit of $61,921.37.
Consequently, the sportswear manufacturer would order fewer sunglasses from their manufacturing plant, relative to chapter 4.
In chapter 6, the expected sales are exactly the order quantity and there is no expected leftover inventory and no expected lost sales. In addition, the sportswear manufacturer would make less profit because instead $6 per cost for the Integrated Firm, the cost of 3D printing are higher with $20. This means that costs are higher and profits are lower.
In chapter 4, the expected profit is the difference between the underage cost times expected sales and overage cost times expected leftover inventory. In chapter 6, the profit is the difference between quantity and the profit pro unit.
7. Competitive benchmarking
To benchmark with the competition, I gave the CEO and example of a company whose business model is similar to chapter 6 and explained why that is the case.
Dell has a similar business model to chapter 6 because it innovates the business model by re-sequencing the operational process to manage better the risk involved. Re-sequencing the process means that Dell assembles to order and do not produces in advance. Dell purchases components and once sales are made, it only then assembles (Traditional: assortment decision -> production -> sales vs. Dell: component assortment decision -> sales -> production). The mechanical engineering department proposes a similar offer by only 3D printing the sunglasses for the sportswear manufacturer on the spot when sales are made for the program. This leads to zero mismatch between supply and demand for both, Dell and the sportswear manufacturer. It reduces risks in the system because no labour has been involved yet before sales. In addition, the usage of further components from third parties helps to pool the risk. Specifically in the case of 3D printing no labour is involved before sales; only 3D printing material in the form of unprocessed powder is sourced from third party vendors.
Furthermore, Fuji has a similar business model to chapter 6 because it innovates the business model by reallocating risk through servitization. Fuji allows its customers to pay per page and only what the customer prints. Similar to that the mechanical engineering department only 3D prints the sunglasses for the sportswear manufacturer on the spot when sales are made for the program and only charges a fee per sunglass. This means the customer and the sportswear manufacturer pay for the function of the equipment and not the equipment itself; in which the equipment in chapter 6 can be investments in the sunglass production equipment of the manufacturing plant. Therefore, the incentives of the two sides are aligned by sharing the risk. For the customer and the sportswear manufacturer, respectively, this means that they do not own all risk, instead share the risk with Fuji or the mechanical engineering department.
Thanks for reading! Liked the author?
If you’re keen to read more of my Leadership Series writing, subscribe and get an email whenever I publish an article of this weekly newsletter.